整数 の 計算 196005-整数の��算 4年 プリント
1 割られる数 = 割る数 × 商 余り 2 余りによる整数の分類 3 整数の割り算と商および余りの説明のおわりに 割られる数 = 割る数 × 商 余り 13 ÷ 2 という割り算について考えましょう。 小学校で習った答え方であれば、 となりますが、高校数学では のように、割り算の計算記号を用いずに、掛け算の計算記号を用いて割り算を表現します。 つまり、 割られる数 = 割る数 × 商 余り② 計算のしかたを考えましょう。 ・整数どうしの計算になるように,わられる数と わる数をそれぞれ10倍します。 42÷35= 42 ÷ 35= ・わり算では,わられる数とわる数に同じ数をかけても商は変 か エクセルで整数とルートのかけ算を行う方法です。 エクセルでかけ算を行うときには、乗算記号「*」を使って、「=2*3」という計算式を作成します。 ルートを含んだ計算の場合も同様です。 √2に整数の3をかける例で確認してみましょう。

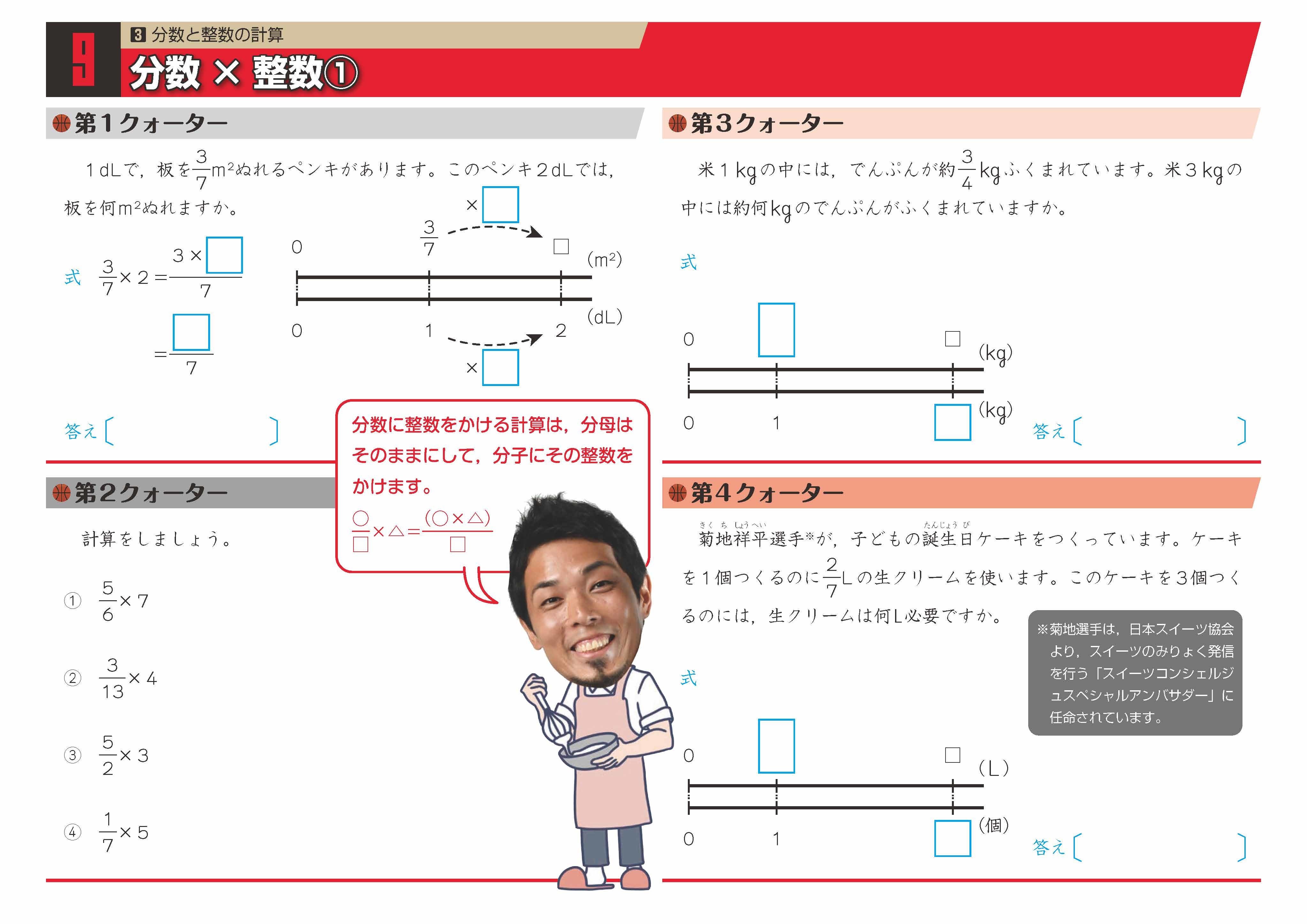
小学6年生の算数 分数と整数のかけ算 分数 整数 整数 分数 練習問題プリント ちびむすドリル 小学生
整数の計算 4年 プリント
整数の計算 4年 プリント- 整数の性質|n進法の四則計算について 今回はn進法の四則計算について学習しましょう。 10進法での四則計算に慣れ親しんでいるので、2進法や3進法で表される数を使って四則計算する場合、思っている以上に計算ミスをしやすくなります。 どの辺りが 整数の計算の文章題 基本から中学入試レベルまで対応して整数の計算の文章題を随時アップしていきます。 たし算、ひき算、かけ算、わり算と分けて問題を作っていませんので、どの式を作るかをお子さんが考える必要があります。 中学受験を考えている小学校3〜4年生のお子さん、文章題が苦手な高学年のお子さんは是非このプリントで練習をしてみて




小数のわり算は整数にして計算しよう 小5向けの動画です Studychannel スタディチャンネル 勉強が楽しくなる 学び 動画サービス
⑤ f (a)を整数係数多項式とすると f (a) ≡ f (b) f ( a) ≡ f ( b) (合同式の多項式) 合同式は 和 、差 、積 、累乗 、多項式 において「=」と同様の計算をすることができます。 しかし「わり算」は特別なので注意しましょう。 注意 合同式の商(わり算)は特殊な場合しか成り立たないので注意してください。 以下が特殊な成立する場合です。 aとnが互いに素のとき a× b ≡ a× c (mod n) a × b分数÷整数 の計算 分数÷整数の計算も、割る数を逆数にして掛けるという考え方は変わりません。整数は分母が 1 の分数とみなすことができるので、その逆数は ~分の 1 の形になることを確認しておき小学5年生で習う「分数÷整数」のわり算と、6年生で習う「分数÷分数」のわり算の計算方法を確認して、繰り返し練習できるプリント。 無料ダウンロード・印刷できます。 (プリント5枚) 小学6年生の算数 帯分数と分数のかけ算 練習問題プリント 小学6年生で習う「帯分数のかけ算」を繰り返し練習できる問題プリント 無料ダウンロード・印刷 (プリント5枚) 小学6年生の算数 帯分数と分
整数と分数の引き算は、整数を分数に直してから計算します。 1 − 1 3 ※引く分数が 1 3 なら 1 = 3 3 、 1 5 なら 1 = 5 5 のように整数を分数に直す = 3 3 − 1 3 = 3 − 1 3 2 3 整数と分数の足し算もやってみましょう。 整数と分数の引き算と同じように、整数を分数になおしてあげます。 3 1 4 ※この場合整数に足し算する分数が 1 4 ですから、最初の 3 を 3 = 3 × 4 4算数・数学の計算が簡単にできるサイトです。 面倒な計算も簡単な入力だけで計算します。 宿題やテストの答え合わせなどに 「算数の電卓」をご活用ください。 URLコピー 計算 整数 奇数・偶数 倍数 公倍数 最小公倍数 約数 公約数 最大公約数 逆数 素数 因数 素因数分解 ユークリッドの互除法 一次不定方程式 分数 図形 円周の長さ 四角形の面積 三角形の面積 台形の面積 平行四辺形の面積 ひし形の面整数×分数のやり方は「A×B/C=AB/C」のように計算します。 整数は分数の「分子」と掛け算します。 また、整数と分数の分母が「約分」できるなら、できるだけ簡単な形に直します。 なお「A=A/1」なので「A/1×B/C」のように分数同士の掛け算として計算することも可能です(当然、結果は同じです)。 今回は、整数×分数のやり方と計算、割り算の仕方、問題の
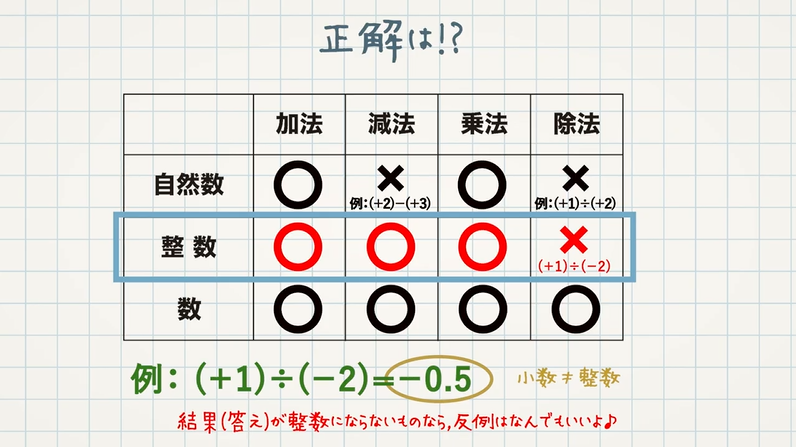
整数 の足し算と引き算だけで 整数 の 平方根 を計算するJavaのプログラムを解説します。 ここで紹介する 平方根 の計算は、与えられた 整数 の 平方根 の 整数 部を求めるもので小数点以下は切り捨てです。 ここから平方根を求める方法について説明し整数の場合 整数の範囲ではどの計算が出来て、どの計算が出来ないのか調べてみましょう。式の値に適当な整数を入れ、その答えがどんな場合でも整数になれば、整数の範囲のみの計算が出来るということが確認できます。 加法では \(3(4)=1\) \((3)(9)=12\)小数点を無視して整数の掛け算として解く 小数点以下の桁数に応じて答えの小数点を移動させる たとえば 252× 31 252 × 31 の場合。 小数点を無視して整数として計算すると、 252× 31=7812 252 × 31 = 7812 小数点以下の数字の個数は計 3 3 つなので、 7812 7812 の小数点を 3 3 桁移動させて 7812 7812 となる。 小数点の処理はこれだけで解決するので、実質整数の掛け算とたいして 違い




小数のわり算は整数にして計算しよう 小5向けの動画です Studychannel スタディチャンネル 勉強が楽しくなる 学び 動画サービス



みんなの算数オンライン 教科書レベル 6年 整数と小数と分数の混ざった計算 整数と小数と分数の混ざった計算 トレーニング
小学4年生の算数・小数のわり算筆算十分の一までの小数÷1桁の整数問題プリントを無料ダウンロード・印刷できます。 (プリント5枚) 小学4年生の算数 小数のわり算|筆算|千分の一までの小数÷2桁の整数 練習問題プリントどちらの考え方で計算しても答えは同じになりますが,(考え方2)のように,計算の途中 で約分するほうが,簡 かん 単 たん に計算できます。 (考え方3) 6 7 ÷2= 6÷2 7 = 3 7 (考え方3)でわられる数の分子が整数でわりきれないときは,分母と分子に建築学生が学ぶ構造力学のPDF版の学習記事 整数×ルートのやり方は? 計算方法 整数(A)×ルートの値(√B)は「A×√B=A√B」になります。 ルートの前に整数の値を書くだけです。 これ以上簡単な数にできません。 なお、ルートの前につく整数を「√の中に」入れることが可能ですが(A√B=√ (A^2B))、できるだけ√の中の数(文字)は、√の外に出した方が




入試に出た計算シリーズ整数計算パック 受験アラカルト ほしい単元だけえらべる教材



1
にすれば,整数の計算と同じように計算 することができるわ。 その通りですね。 01や001のいくつ分と 考えるといいですね。 28 28 168 28 168 小数点を考えないで たてにそろえてかく。 整数と同じように 計算する。 小数点 をうつ。 25 3 75 6 15 15ルートを整数にするためには、中身を2乗の形にする必要があります。 ですが、2と3がそれぞれ2乗になっていません! 困った! ということで、 のところに2と3を1つずつ入れてあげれば全部を2乗の形にすることができますね。 こんな感じ! というわけでA ≡ a' (mod 256) b ≡ b' (mod 256) が成立します。 一方 a b ≡ a' b' (mod 256) a b ≡ a' b' (mod 256) a * b ≡ a' * b' (mod 256) が成立しますから,左辺の結果が8ビット整数の範囲にあれば,右辺の結果の補数表示として得られます。 4.結果が範囲外になる計算の場合は,一見おかしな結果が得られます。 例えば,今の場合(8ビット),128 は 128 を表しますから, 1271 = 128 と




帯分数の計算方法と仮分数への書き直し方



3
実数 √(ルート)の整数部分と小数部分の計算はこれで十分の巻 vol10: 3回読めば、絶対理解できる看護受験数学 いくつか 出題されるパターン が決まっています。 を聞かれることも多いです。 理解してもらっています。 それだけ 落としたくない問題 でもあります。 それでは、√(ルート)の「整数部分」と「小数部分」をみてみましょう。一.整数の計算 (小1~5年) ・百ます計算 ・足し算・引き算の筆算 ・掛け算・割り算の筆算 ・計算の順序 ・偶数・奇数・約数・倍数 ・素数・素因数分解・累乗 ・公約数・最大公約数の求め方 ・公倍数・最小公倍数の求め方 こんにちは、年齢 3X 歳の peria です。 6月に @square1001 さんの「超高速! 多倍長整数の計算手法」シリーズ(前編 / 後編) が投稿された際、Constants コンテスト で数年前に得点していたことを思い出しつつ、今だともう少し書けるかな、というノリだけで色々コーディングしていたら総合2位まで来た




すきるまドリル 小学6年生 算数 分数のかけ算 無料学習プリント すきるまドリル 幼児 小学生の無料学習プリント



数の集合と四則 教遊者
分数を整数に 後者の分数を整数にするために、分母と同じ数、つまり3を両者にかけましょう。 15:10/3 =45:10 これで、土台作りが完了しました。あとは約数で割るだけの作業ですね。 45:10 =9:2 いかがでしょうか。かけられる数の分子(上)に整数をかけた数になっています。 計算の途中で約分できるときは 約分します。 教え方2 分数÷整数の教え方 かべにペンキをぬる面積から、分数のわり算の問題を理解させ、分数÷整数の式の意味と計算のしかたを教えます。 問題1整数と小数の計算① 整数と小数の計算② 整数と小数の計算③ 整数と小数の計算④ 計算プリントcomの問題はすべて無料です プリントなどについて



整数の計算 リーディングス新しい算数研究



しょうちゃん 公式ブログ Snsで見かけた算数の問題を解いてみる その10 整数の計算 Powered By Line
Java Javaのプログラムでは、整数と小数点を一緒に計算する際、小数点以下を切り捨て、整数として答えを算出できる方法があります。 キャストと呼ばれる型変換の機能を利用することで、いとも簡単にdouble型 (少数点)の数値をint型 (整数)の数値に変えながら計算してしまえるのです。 (int)(整数 任意の演算子 小数点) //整数・少数点の位置は逆でもOK CopyJava で for ループを使って整数の長さを計算する まず、これに対する単純な反復ソリューションを見ていきます。 整数を 10 で除算し、数値がゼロになるまで各反復でカウントを保存します。 以下のコードは、上記の方法を示しています。 Java java Copy 剰余の計算方法 = / とするとき、 = ( * ) で表せる 例として、 = 42 = 7 とすれば、 = 42 / 7 = 6 = 42 (6 * 7) = 0 となる 商が整数とならない場合における、剰余のバリエーションがこの記事の



1



1
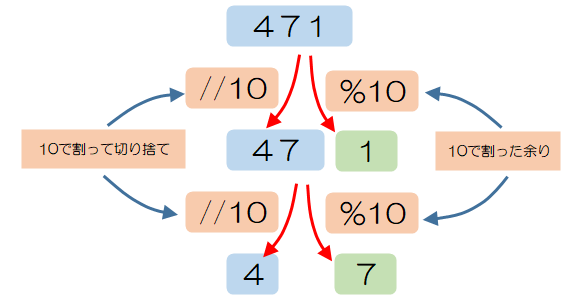
やはり言葉の式では 全体の量÷人数=ひとりぶん量 となることに気づかせます。 すると 式は 08÷4 となります。 考え方 08÷4の計算の仕方は 08は01が8こ と考えます。 8こ÷4は 2こですから 08÷4は、01が2こになります。 08÷4 =02 答え 02L この考え方を下の図を見せてよく説明します 次に、上の考え方をもとに、84÷3の計算のしかたを気づかせます 84÷3の計算の仕方は 84は整数の計算の文章題 整数の文章題2 gのかごに、1こ gの玉を こ入れると、全体の 重さは何gになりますか。 式 答え g ある中学校の生徒数は、1年生が 人、2年生が 人、 3年生が 人で、女子生徒は 男子生徒は何人ですか。 式 答え 人整数の計算方法は 10進数からn進数への変換(整数) で解説した方法になります。 10進数の「525」を2進数に変換 <整数部> <少数部> 525 (10) = (2) 整数は下から上、少数は上から下に並べることに注意してください。 少数の10進数を16進数に変換する場合も計算方法は同じです。 ただし10進法よりも大きい16進法はアルファベットを使いますので、整数が9よりも大きくなった場合は




小学6年生 分数 整数の計算 学童cafe チャイルドスペース



6年算数 分数 整数 分数 整数 教え方のポイント
一の位が5の二桁の整数の2乗の速算の証明 ヒロ 証明しておこう。 証明 ( 10 a 5) 2 = 100 a 2 100 a 25 これを次のように変形するのがポイント。 ( 10 a 5) 2 = 100 a ( a 1) 25 これは a ( a 1) を100倍して25を加える計算だから,下二桁は必ず25になる整数部関数は、引数に指定された数値の整数部分のみを取り出す関数です。 小数点以下がある場合は値以下で最大の整数を返します。 整数というのは具体的に言うと、0や負の数、また小数や分数ではない数値になります。 例えば数値が15ならば、整数部関数を使うと整数部分が返ってくるので1になります。 整数部関数は四捨五入や、端数の切り捨てなどによく




整数計算とforループ 九九の表を作ってみよう Objective C の動画チュートリアル Linkedinラーニング




小6算数 大日本図書 分数と整数のかけ算 わり算 Youtube




小5算数 帯分数 整数 Youtube



小学生の自宅学習 小学6年生算数編 プロバスケ選手が教える 算数ドリル講座vol 7分数と整数の計算 分数 整数編公開のお知らせ アルバルク東京



つまずきをなくす小3算数計算 整数 小数 分数 単位 改訂版 通販 セブンネットショッピング
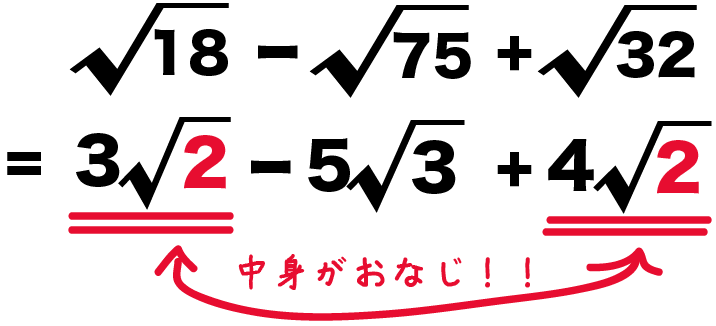



平方根 ルート の足し算 引き算の仕方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



反転授業 小学4年生 計算の工夫 小数編 ふるやまんの算数塾




Bashで簡単な計算 をする一番良い方法はこれ Lfi



小数 整数の計算のやり方 大人のやり直し算数の第一歩 計算方法の解説 無料




基礎から分数4 整数と分数を足したり引いたりの計算 都立入試の情報満載 こじんまりしたこじま塾ブログ



小数 整数の計算のやり方 大人のやり直し算数の第一歩 計算方法の解説 無料




小4算数 小数のかけ算とわり算を考えよう 学習プリント 練習問題 無料ダウンロード印刷



小数 整数の計算のやり方 大人のやり直し算数の第一歩 計算方法の解説 無料



分数の引き算 整数から



03 分数と整数のかけ算




分数のひき算 整数ひく真分数 小学4年生算数 無料プリント
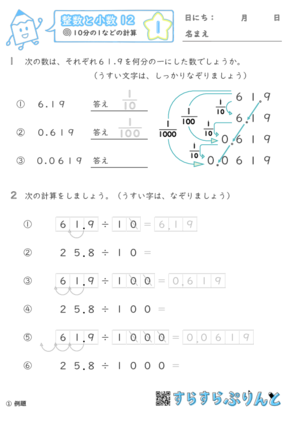



整数と小数 小学5年生算数 無料プリント教材




ヨドバシ Com 整数の計算 リーディングス 新しい算数研究 1 全集叢書 通販 全品無料配達




3年生の計算 整数の計算すべて 50枚 メルカリ
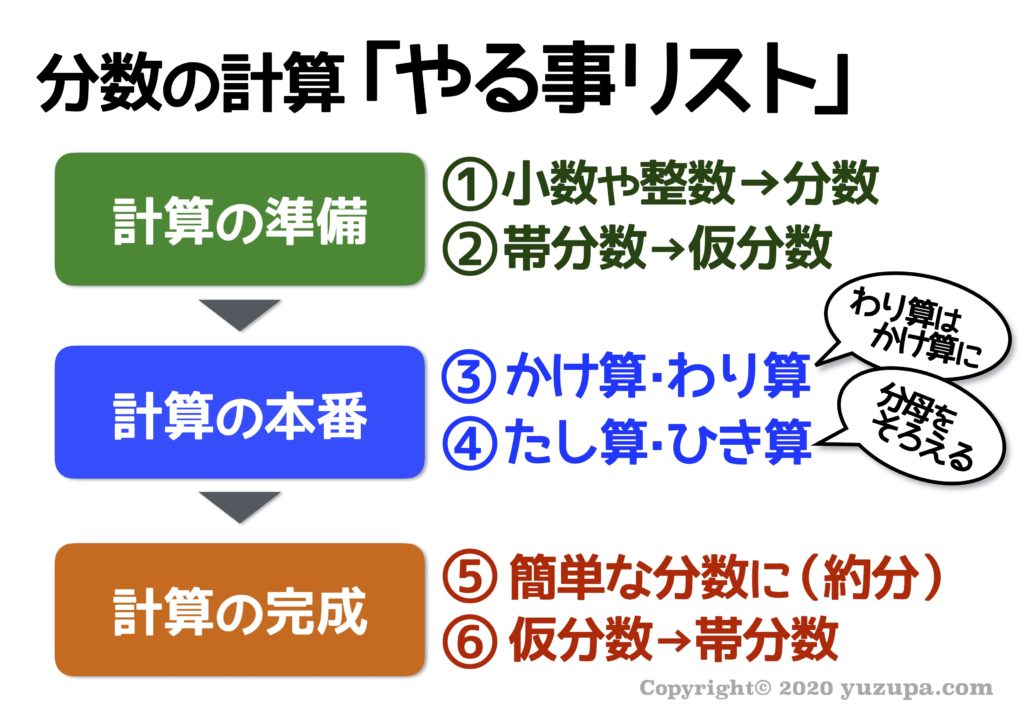



中学受験 分数の計算で間違え連発 やる事リスト で驚くほど上達 かるび勉強部屋




小学5年生向け分数のかけ算問題
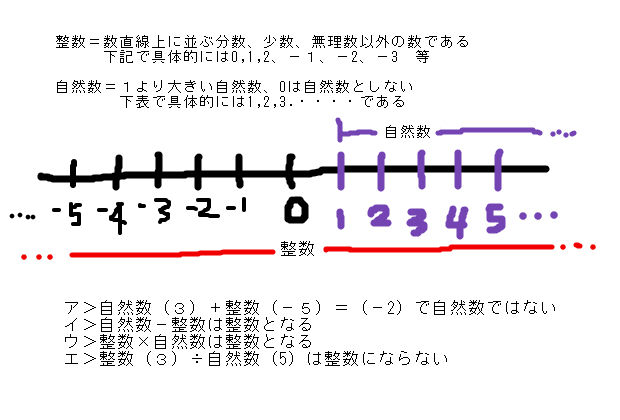



自然数と整数の四則計算の結果の問題 中学 数学 理科の復習サイト




3年生の計算 整数の計算すべて 50枚 メルカリ



小数 整数の計算のやり方 大人のやり直し算数の第一歩 計算方法の解説 無料




分数のかけ算 分数と整数の積 積が整数 小6 学習プリント



実数とは 0 は実数 定義や記号 虚数との関係や計算方法 受験辞典




世界一分かりやすい算数 小4 小数 整数 小数 整数
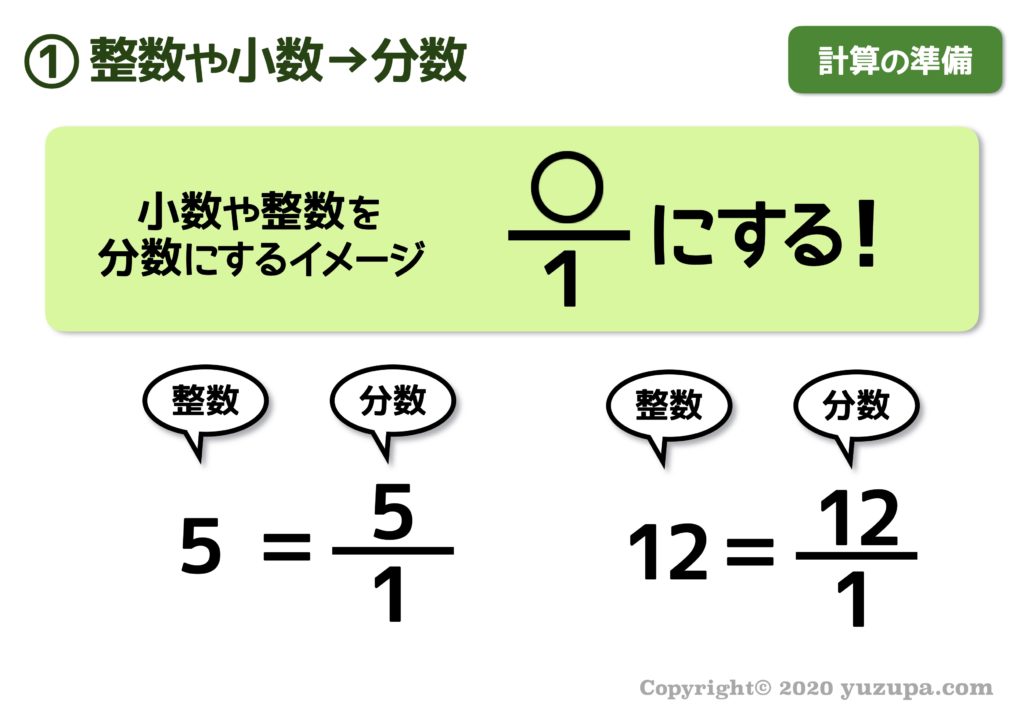



中学受験 分数の計算で間違え連発 やる事リスト で驚くほど上達 かるび勉強部屋



整数 ルートのやり方は 1分でわかる計算 割り算 ルートの掛け算 足し算



03 分数と整数のかけ算




Double型の小数点を切り捨てint型の整数と一緒に計算する方法 Java 文系エンジニア



4年算数小数 整数 小数 整数 1 教え方




C言語チャレンジ 整数の計算 電脳産物




つまずきをなくす小3算数計算 整数 小数 分数 単位 改訂版 通販 セブンネットショッピング




超高速 多倍長整数の計算手法 前編 大きな数の四則計算を圧倒的な速度で Qiita




学習のポイント 小数 整数 の意味と計算の仕方について理解し学習していきましょう 0 1を単位として考え 小数のわり算は整数と同じように考えて 計算しましょう 小数 整数 の計算を 筆算を使って計算できるよ 小学校 算数 学習 小数




整数の計算 意味がわかる小学算数1日目 Youtube
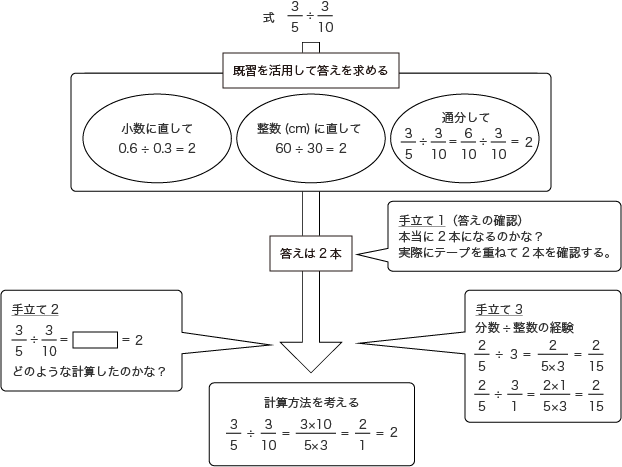



算数実践実例集 啓林館



3 23第1章式の計算の利用 整数の性質の証明




数基礎 Com 整数と分数が混ざった計算が分かる方法



3分でわかる 整数と分数の計算方法 インターネット家庭教師のアスミラ



小数 整数の計算のやり方 大人のやり直し算数の第一歩 計算方法の解説 無料




小学5年生 小数 整数の計算 学童cafe チャイルドスペース



記事 詳細情報 年 5月 25日 月曜日 6年生 算数 先生たちからのプレゼント 算数の学習では 対称な図形の学習の後に分数 整数 分数 整数の計算の仕方の学習が始まります そこで 計算の仕方を載せますので できる人はチャレンジしてみて
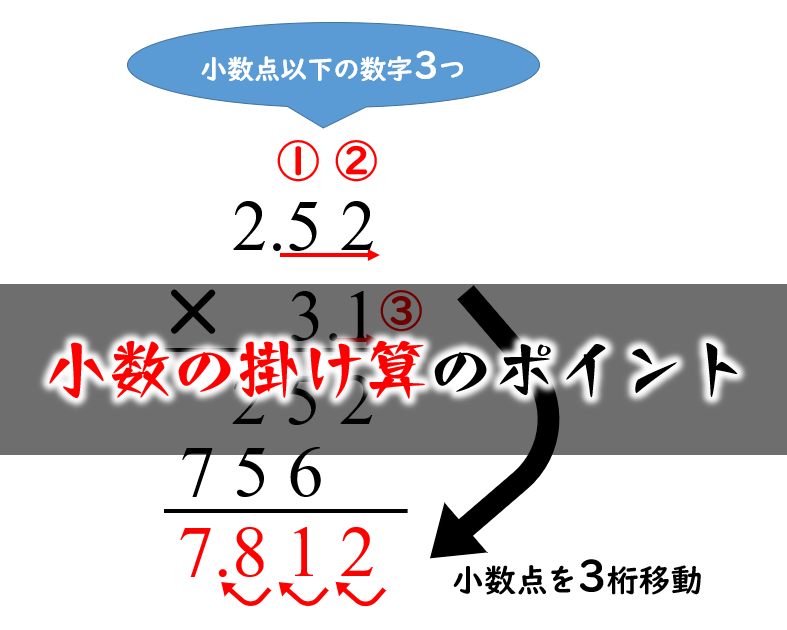



小数の掛け算の計算手順 小学生に分かりやすく教える方法 数学fun



小数 整数の計算のやり方 大人のやり直し算数の第一歩 計算方法の解説 無料
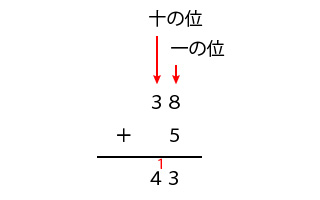



たしざんの計算方法 整数の普通の計算 もう一度やり直しの算数 数学




分数の文字式と整数の掛け算 よく使う非常に大切な知識 中学や高校の数学の計算問題




小数 分数 整数のまじった計算はこうする 小6向けの動画です Studychannel スタディチャンネル 勉強が楽しくなる 学び 動画サービス




3年生の計算 整数の計算すべて 50枚 メルカリ




Php 割り算 小数点まで計算 余り計算 整数で終わり だよって話




小学6年生の算数 分数と整数のかけ算 分数 整数 整数 分数 練習問題プリント ちびむすドリル 小学生




分数の掛け算は なぜ分母同士 分子同士を書けるの 元小学校教師が教える できる子ども育成塾 小岩 小学生専門の個別指導塾




整数をルートにする方法 5秒で計算できる簡単な問題だ 中学や高校の数学の計算問題



オール整数計算 版 Buyee Buyee Japanischer Proxy Service Kaufen Sie Aus Japan
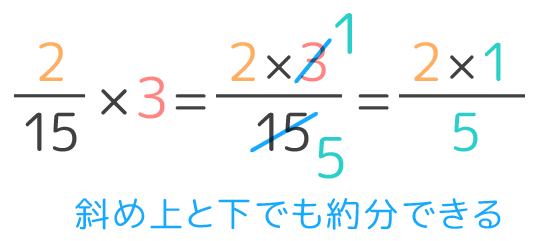



小学5年生 帯 真 分数と整数の割り算 を図解 そうちゃ式 分かりやすい図解算数 別館
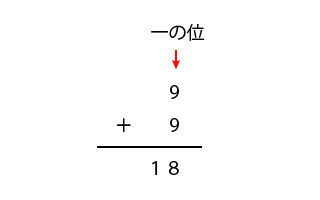



たしざんの計算方法 整数の普通の計算 もう一度やり直しの算数 数学




分数のかけ算 分数 整数 算数 数学が好きになりmath




小学5年生 整数 小数の計算 学童cafe チャイルドスペース



小数 整数のかけ算のやり方 大人のやり直し算数の第一歩 計算方法の解説 無料




小数 整数 の筆算のしかたを説明しよう 光輝学園つくば市立葛城小学校



小数 整数のかけ算のやり方 大人のやり直し算数の第一歩 計算方法の解説 無料




整数の計算表 平方 立方 平方根 立方根並に逆数整数10 000まで 1957年 東京工学研究会 本 通販 Amazon




整数 分数 小数の混じった計算 Youtube




整数とは 小学生でも簡単にわかる問題で 違いを覚えよう 中学や高校の数学の計算問題




小学校4年 算数 小数 整数の計算 小数 整数の筆算2 Youtube



整数の計算 割り算 の計算結果がおかしい Fms Programming




分数 整数 の掛け算 計算ドリル 問題集 数学fun




速算 二桁の整数の積を速く計算する方法 証明付き 大学入試数学の考え方と解法



Tufs Ac Jp



4年算数小数 整数 小数 整数 1 教え方




分数と整数のかけ算 Twitter Search Twitter



6年生 分数 整数の計算に挑戦しよう 高岡市立福岡小学校




整数と小数 10倍 100倍 1000倍の計算 小学5年生算数
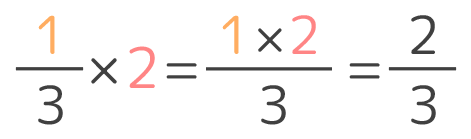



小学5年生 帯 真 分数と整数のかけ算 を図解 そうちゃ式 分かりやすい図解算数 別館




分数のかけ算 整数 分数 算数 数学が好きになりmath



Pythonによる四則演算と分数の計算




中学受験講座 分数の計算 かけて整数になる計算 Youtube



小数 整数の計算のやり方 大人のやり直し算数の第一歩 計算方法の解説 無料
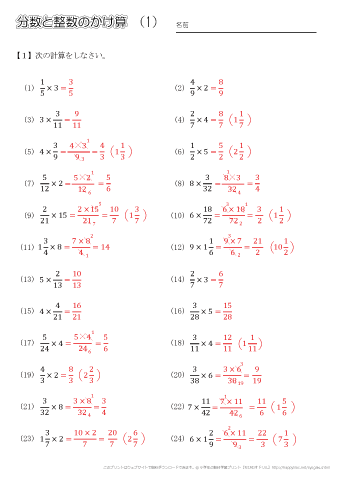



小学6年生の算数 分数と整数のかけ算 分数 整数 整数 分数 練習問題プリント ちびむすドリル 小学生




正負の数 剰余 整数 問題 001 100




小4 算数 計算 無料プリント ひっ算 小数と整数のわり算 小数 1けたの整数 むげんプリント
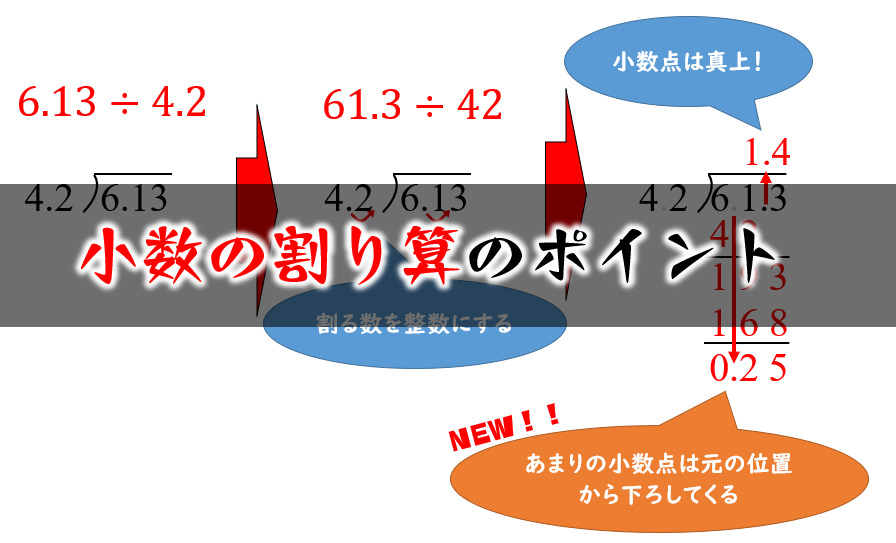



あまりが出る小数の割り算の計算手順 小学生に分かりやすく教える方法 数学fun




小5算数 小数のかけ算 指導アイデア みんなの教育技術




つまずきをなくす 小3 算数 計算 整数 小数 分数 単位 西村則康 本 通販 Amazon




小学6年生の算数 分数 整数のかけ算 練習問題プリント ちびむすドリル 小学生



いろいろな計算 整数 a4版 小3 4 Buyee Buyee Japanese Proxy Service Buy From Japan Bot Online




分数の掛け算は なぜ分母同士 分子同士を書けるの 元小学校教師が教える できる子ども育成塾 小岩 小学生専門の個別指導塾
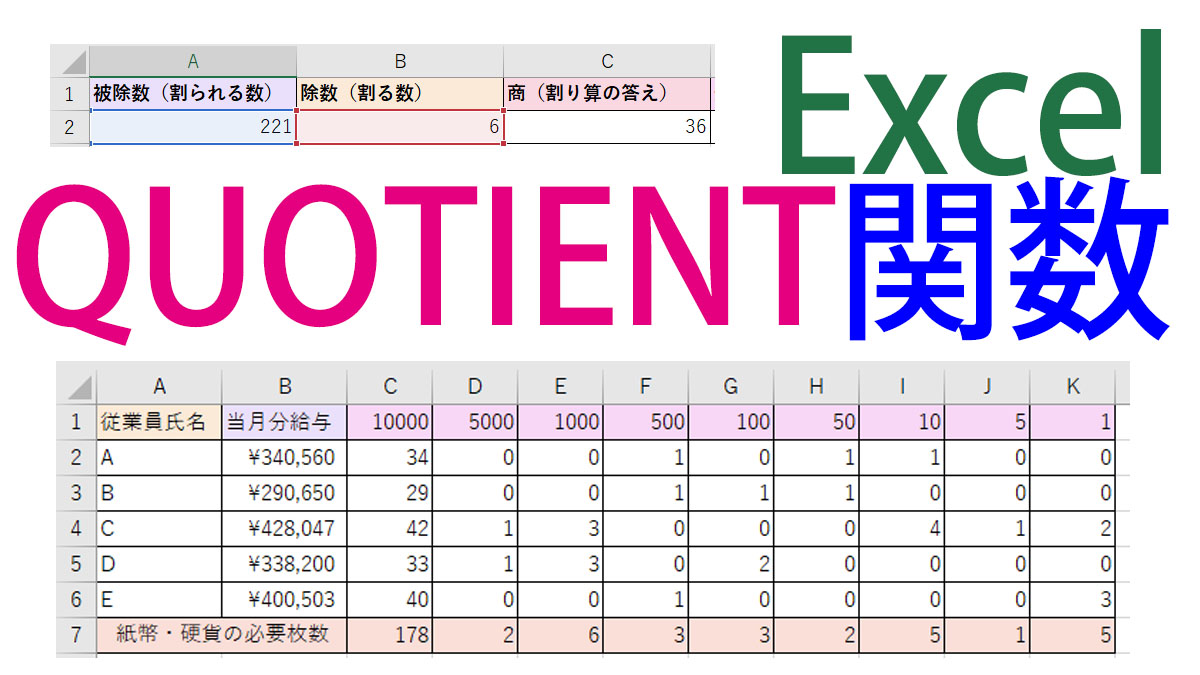



Excel エクセル Quotient クオーシェント 関数の使い方 割り算の商を整数で計算 Tschoolbank 作 るバンク



小数 整数のかけ算のやり方 大人のやり直し算数の第一歩 計算方法の解説 無料
コメント
コメントを投稿